A XV. század közepén, Gutenberg találmányával az információtörténetnek új korszaka kezdődött. Az írott, gazdagon díszített kézírásos kódexek helyét fokozatosan elfoglalta a nyomtatott könyv. Északon a népmozgalmak, a reformáció, délen a reneszánsz szelleme, a felvilágosodás igényelték a könyvet. Az Európa-szerte kifejlődő és alakuló egyetemek szükségszerűen sok könyvet igényeltek. A haladás egyik követelménye az volt, hogy olyan technikát alakítsanak ki, amellyel a hiteles szöveget több száz vagy több ezer példányban egymással teljesen azonos formában tudják kibocsátani. Másolással ez nem volt megoldható. A kézzel írott és nyomtatott könyvek között az átmenetet a fametszetű nyomatok képviselik.

 

76. kép: Fametszet - Szent Antal

 

http://www.mke.hu/lyka/13/435-450-metszet.htm

A fametszést már a XIII. században ismerték, a XV. sz. első felében már fatábláról nyomtatott képeskönyvek is megjelentek.

 

77. kép: Fametszés

 

A legelső tömeges könyvsokszorosítás kísérlete L. J. Costernek, a hollandiai Haarlemben működő fametszőmesternek a nevéhez fűződik.

 

78. kép: Laurenz Janson Coster holland fametszőmester

 

L. J. Coster Donatus ezeréves latin nyelvtanát fatáblába metszette, s erről nyomtatott 32 oldalas füzeteket. Nagyobb terjedelmű szövegek elkészítésére azonban ez az eljárás nehézkes és kivihetetlen volt.

 

79. kép: Aelius Donatus - Ars Grammatica

 

http://www9.georgetown.edu/faculty/irvinem/articles/bookfutures/

Az ókori és középkori mesterek sok évszázaddal a nyomtatás feltalálása előtt nyomtattak pecsétnyomókkal és hengerpecsétekkel monogramszerű írásjeleket. A XII. sz. könyvkötői különleges acélbélyegzőkkel díszítgették a könyvtáblákat és különálló acélbetűikkel préselték a kötések bőrtábláira a könyv címét. Éremkészítők és aranyművesek már régebben készítettek feliratokat és díszeket keményebb fémbe vésett mintabetűknek és ornamenseknek fémbe való ütögetésével. Amikor Gutenberg a patricát (az acélpálcikába faragott betűt) puhább fémbe préselte, megszületett a matrica. Ez azonban még nem oldotta meg a betűöntés kérdését: azt, hogy a szedésben a betű képe vízszintes vonalban álljon egymás mellett, hogy minden egyes betű olyan széles testre legyen öntve, amilyent rajza megkívánt, hogy minden betű azonos magasságú legyen. Gutenberg fölfedezésének lényege a betűk sorozatgyártása, amely által lehetővé válik szövegek kiszedése, majd a sajtó felhasználásával ezekről több azonos példány készítése. Valójában ő fejlesztett ki elsőként olyan, mozgatható betűelemeken és nyomógépen alapuló módszert, amellyel sokféle írott anyagot lehetett gyorsan és pontosan kinyomtatni.

 

80. kép: Betűk sorozatgyártása

 

A modern értelemben vett könyvnyomtatásnak négy alapvető összetevője van. Az első a mozgatható betűminta néhány egyéb művelettel együtt, melyek során a mintákat elhelyezik és rögzítik. A második a nyomógép maga. A harmadik a megfelelő nyomdafesték, s az utolsó a megfelelő anyag, mint amilyen a papír, amelyre nyomtatni lehet. (A papírt Kínában Caj Lun nevű hivatalnok már Kr. u. 105 körül feltalálta.) Gutenberg a nyomtatás lényeges elemeit tökéletesítette; létrehozott egy betűmintához alkalmas fémötvözetet, egy hibátlan öntőformát, egy olaj alapú nyomdafestéket, és egy nyomtatásra alkalmas gépet. Találmánya azért kiemelkedő jelentőségű, mert a nyomtatás elemeinek összekapcsolásával a gyártás új, hatékony rendszerét alakította ki. Gutenberg a nyomtatás teljes gyártási folyamatát találta fel, neki köszönhetjük a könyvnyomtatási technológiát, amelynek jelentősége a tömegtermelésben van. Ezen időszakot gyakran, és jogosan az első információrobbanásnak is nevezik.

Johannes Gutenberg, eredetileg Gensfleisch néven, a németországi Mainzban született 1400 körül. A patrícius családból származó nyomdász már az 1430-as évek végén kísérletezett a nyomtatással, de nyomtatványai csak az 1440-es évekből ismeretesek. Találmánya alkalmazásának pontos időpontja ismeretlen, ezért a könyvtörténeti kutatók az 1440-es esztendőt fogadták el nemzetközi közmegegyezéssel. Az általa nyomtatott kiadványok egy része kis terjedelmű munka volt: népkönyvek, kalendáriumok, búcsúlevelek, imádságok, latin nyelvkönyvek, s egy papi bulla. Főműve a napjainkban is az egyik legszebbként számon tartott nyomdai munka, a kézi festéssel gazdagon díszített, 42 soros Biblia, amely 1450-1456 között készült. Talán 1468-ban halt meg, Mainzban. Találmánya rövid időn belül Európa számos országában ismertté vált.

 

81. kép: Johannes Gutenberg (1400 körül-1468) fametszetű fantázia-portréja

 

Mai tudásunk szerint 1500-ig 18 ország 260 városában 1125 nyomda működött, az általuk megjelentetett művek száma mintegy 40.000 „kötet" volt. Az információfeldolgozás technikáját illetően, fontos tudni, hogy a könyvek, később egyre nagyobb jelentősséggel bíró címlapja, lényeges adatokat tartalmazó kolofonja, tartalomjegyzéke is egyre fejlettebb lett, és széles körben elterjedt az oldalszámok használata is. (Az első nyomtatott címlap 1463-ban egy pápai bullán jelenik meg.) Németországban 1489-ben megjelennek az első nyomtatott plusz és mínusz jelek, 1500-ban pedig az írásjelek között megjelenik a zárójel is.

Ebben az időszakban a nyomtatásnak köszönhetően, Angliában és a kontinensen már legalább 20 „newsbook" adott tájékoztatást, információt, a fontosabb eseményekről és közügyekről. 1507. április 25-én adta ki a német Martin Waldseemüller freiburgi térképész az új világtérképet, amelyen első alkalommal szerepelt az „America" név a mai Brazília helyén szereplő földrészlet jelölésére. Waldseemüller az újonnan felfedezett kontinenst Amerigo Vespucci-ról, a felfedezőről és tengerészről nevezte el, aki írásaival, úti beszámolóival évtizedeken formálta a kontinensről alkotott képet. Vespucci, a firenzei üzletember, szerencséjét a könyvnyomtatás hozta meg, ennek révén váltak írásai szabályos bestselleré. Az Amerika név igen hamar elterjedt, és átvette a flandriai Gerhard Mercator is, akinek 1569-ben jelent meg a világtérképe, az új vetületi ábrázolással. 1570-ben jelenik meg az antwerpeni Abraham Ortelius könyvillusztrátor Theatrum Orbis Terrarum c. atlasza, amelyhez névmutatót készít, és amelyben egy magyar rézmetszet is helyet kap, ez a Zsámboky-féle Magyarország térkép. Itt jegyzem meg, hogy a vizualizáció, a térképtörténet fontos fejezete lenne az információtörténetnek.

 

82. kép: Abraham Ortelius (1527-1598) világtérképe, a Typus orbis terrarium

 

Az új típusú információhoz különféle információs szolgáltatások is társultak. I. Miksa német-római császár még 1494-ben egy rendszeres futárszolgálat létrehozásával bízta meg főpostamesterét, Franz von Taxis grófot, akinek a postajáratok és hálózatok létrehozását tulajdonítjuk. A gróf, aki 1500-tól főpostamestere volt Szép Fülöpnek, Kasztília királyának és Németalföld, valamint Burgundia uralkodójának, a 15-16. század fordulóján a fontosabb útvonalak mentén postamestereket alkalmazott. Megindult a postaforgalom szerte a Birodalomban, s Németalföld, a bécsi, francia és spanyol udvar között. A postamesterek fogadták és indították útnak rendszeres időközökben azokat a lovas hírmondókat, kurírokat, akik által sok érdekes hír birtokába jutottak. Az üzleti érzékkel rendelkező postamesterek azután ezeket az összegyűlt értesüléseket levél formájában maguk továbbították megrendelőiknek, rendszeres időközökben. Természetesen nem csak a kéziratos, hanem a nyomtatott újságok: a nyomtatott újságlevelek csakúgy, mint a későbbi hírlapok is szoros kapcsolatban álltak a postajáratokkal. A postajáratok rendszerré szervezése, a lovas postakocsik „gépesítése" még várat magára, de információtörténeti szempontból a hálózat nagy jelentőségű.

1522-ben jelent meg Luther Márton híres német bibliafordítása, elsőként az Újszövetség. A magyar nyelvű Szent Bibliát, Károli Gáspár fordítását, 1590-ben nyomtatták ki Vizsolyban, talán 800 példányban. Kötetek szólnak erről.

 

83. kép: Vizsolyi Biblia - Károli Gáspár (1529-1591) fordítása

 

Megélénkül persze a szótárkészítés is, 1552-ben elkészül, pl. az Angol-Latin Abecedarium, 1555-ben Conrad Gesner, svájci természettudós összeállítja a Bibliotheca Universalis-t, minden idők íróinak katalógusát. Megnyílik egy-két igazi közkönyvtár, 1571-ben a Mediciek pl., az általuk gyűjtött klasszikus kéziratok és könyvek gyűjteményét hozzáférhetővé teszik Firenze népe számára.

Rendkívüli információtörténeti jelentőségű esemény, amely az időrend megteremtését képes felgyorsítani az információk özönében, az XIII. Gergely pápa (1572-1585) 1582. február 24-én kelt az Inter gravissimas kezdetű bullája.

 

84. kép: XIII. Gergely pápa (1572-1585)

 

Ez egyetlen dolgot változatott a Julius Caesar által Kr. e. 45-ben bevezetett naptáron, csökkentette a szökőévek számát. A Julius Caesarról elnevezett Juliánus-naptár szerint minden negyedik évet szökőévnek kellett tekinteni, míg a Gergely-féle, vagy másképpen Gregorián naptár ezt a szabályt úgy módosította, hogy az évszázadokat záró, tehát századdal végződő évek közül csak azok legyenek szökőévek, amelyeknek számjegye nemcsak néggyel osztható, mint a többi szökőévé, hanem négyszázzal is. (Így 1600 szökőév lett, 1700, 1800 és 1900 nem, viszont újra szökőév lett a múlt századunk utolsó éve, 2000.) Ez az elv visszamenőleg is érvényesült oly módon, hogy úgy tekintették, mintha a Caesar-féle reform bevezetése óta tíz közönséges év lett volna; ezért 1582. október 4-e után 15-ét kellett írni.

Ma is a Greogorián naptárt használjuk, pl. a könyvtári dokumentumok egyes adatainak bibliográfiai leírásakor is. „A megjelenés idejét (egy vagy több dátumát) úgy kell leírni, ahogy a főforrásban szerepel, beleértve a napot és a hónapot is. Ha a megjelenés éve a főforrásban római számmal szerepel, akkor a teljes dátumot a forrásnak megfelelően kell leírni, az évszámot elválasztó szóközök nélkül, és utána szögletes zárójelben kell megadni a Gergely-naptár szerinti évet arab számmal. . . . A maitól eltérő időszámítás szerinti dátumot, valamint a hónapoknak és napoknak a mai számítástól eltérő formáját és nevét úgy kell leírni, ahogyan a főforrásban van, és utána szögletes zárójelben lehetőség szerint közölni kell a mai (keresztény) időszámítás és naptár szerinti megfelelő dátumot."

Az időszámítás és naptárkészítés komoly számolási feladatot is jelentett. Az alapegységek: az év, a nap, és a hónap. Mindez a Föld keringési és forgási periódusa, valamint a Hold keringési periódusa, vagyis egy év, amikor a Nap (Föld) visszatér ugyanoda, pl. a tavaszponthoz kb. 365 nap után, ill. a Hold visszatér valamely viszonyítási ponthoz, pl. az újholdhoz. A naptár alapja az évszakokat meghatározó tropikus (tavaszponttól-tavaszpontig) év, amely 365,2422 nap, ill. a holdfázisokhoz kötődő szinódikus (újholdtól-újholdig) hónap, amely 29,530589 nap. Ezekkel a kérdésekkel részletesebben a matematikai vagy asztronómiai geográfia foglalkozik ma is.

Az információs rendszerek történetében a most tárgyalt korszaknak fontos szerepe van a számolási segédeszközök terén is. Mint korábban említettük, a középkor vége felé Indiában, majd Perzsiában, Kínában és az arab kultúrákban az osztási művelet elvégzésére is képes ún. rácsos módszert alkalmazták. A módszer alapját képező, a szorzási műveletet megkönnyítő gelosia algoritmus Európában a XIV. század elején vált ismertté. A gelosia-módszer egyszerűsítésére John Napier (1550-1617), I. Erzsébet skót udvari tudósa, az algoritmus felfedezője, kis rudacskákat készített. A készlet tíz darab pálcából állt, mindegyik számjegynek volt egy pálca. Egy pálcára egy számjegy többszöröseit írta a gelosia-módszernél szokott módon. Szorzás elvégzéséhez az egyik tényezőnek megfelelő pálcákat rakták egymás mellé, majd a másik tényezőnek megfelelő sorokból a gelosia-módszernél megszokott módon leolvasták a szorzatot.

 

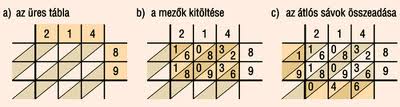
85. kép: Gelosia-módszer

 

Napier kortársa, Gaspard Schott jezsuita szerzetes henger alakú számolópálcákat esztergált, és mindegyiknek a felületére a teljes Napier-féle pálcakészlet tartalmát felírta, vagyis több egyforma hengert készített. Több ilyen hengert egymással párhuzamosan forgatható módon egy keretbe erősített. Az egyes hengerek elforgatásával elérte, hogy ott az egyik szorzótényező számjegyeinek megfelelő számoszlopok kerüljenek felülre, tehát ekkor úgy nézett ki, mintha a megfelelő Napier-pálcákat tették volna egymás mellé. A készülék nem terjedt el a gyakorlatban, alig volt hatékonyabb számolási eszköz, mint az abakusz. Érdekes módon azonban ezt az eszközt még 1885-ben is tökéletesítették: Henri Genaille a Napier-pálcák megfelelő kialakításával és elhelyezésével megoldotta a kétjegyű részösszegek automatikus átvitelének problémáját is.

A logarléc, melynek használata mintegy 300 éven keresztül, a zsebszámológépek megkonstruálásáig szinte egyeduralkodó volt, nem Napier találmánya. A logarlécet 1620-1630 között találták fel, miután John Napier publikálta a logaritmusról szóló alapvető művét. Az oxfordi egyetemen Edmund Gunter (1581 - 1626) feltalált egy eszközt, mely egy logaritmikus skálából és mérőeszközökből állt, és amellyel szorozni és osztani lehetett. 1630-ban William Oughtred (1574-1660) készített egy körlogarlécet és 1632-ben egyesítette találmányát Gunter eszközével, ezzel létrejött a mai értelemben vett logarléc. A logarléc egy egyszerű kivitelű, mechanikus működésű analóg számítógép, amely lehetővé teszi különböző matematikai műveletek gyors, 3-4 számjegy pontosságú elvégzését. Az 1960-as években, az édesapámtól megörökölt, villamosmérnök testvérbátyám által is használt logarléc Faber-Castell verziójával, egyetemistaként az magam is számoltam, mivel a mérnöki számítások túlnyomó részét logarléc segítségével végeztük. Még az Apolló űrhajósai is ezt a számológépet használták.

 

86. kép: Logarléc

 

1623-ban Wilhelm Schikard (1592-1635) tübingeni professzor a Napier-pálcák felhasználásával a négy alapművelet elvégzésére alkalmas számológépet készített. A gép elkészítésére a késztetést valószínűleg a Keplerrel folytatott beszélgetései jelentették. A gépről is csak Kepler iratai között maradt egy vázlat (lásd az ábrát): az eredeti gép a harmincéves háborúban eltűnt, a Kepler számára készített másodpéldány még a műhelyben elégett, Schikard pedig egész családjával együtt meghalt pestisben, mielőtt még egyet készíthetett volna. A vázlat alapján 1960-ban sikerült egy jól működő rekonstrukciót készíteni.

 

87. kép: Wilhelm Schikard (1592-1635) számoló órájának rekonstrukciója

 

A számológép felső része hat darab függőlegesen elrendezett, Gaspard Schott megoldásához hasonló hengeres Napier-pálcát tartalmaz, így legfeljebb hatjegyű számokkal való műveletvégzésre alkalmas. Az egyes számjegyeket a pálcák megfelelő elforgatásával lehet beállítani. A pálcák alatt fogaskerekekből készített számlálómű található. A felhasználónak a pálcákról leolvasott részeredményeket kézzel kellett bevinni a számlálóműbe és azzal összeadni. A számlálómű elvégezte a kétjegyű összeg első jegyének átvitelét is a következő nagyobb helyiértékre: az egyik kerék egy teljes körülfordulása egy külön fog segítségével a következő helyiértéknek megfelelő fogaskereket egy számjeggyel elforgatta (hasonló megoldás látható pl. a jelenleg is használt villanyórákban, gázórákban, kilométer-órákban, stb.). A végeredmény a gép alján lévő kis nyílásokban jelent meg. Schikard külön számtárcsákat is felszerelt a gépre, amelyek megfelelő elforgatásával a legfeljebb hatjegyű részeredményeket lehetett tárolni, megkímélve ezáltal a felhasználót a leírástól. A gép jelezte a túlcsordulást is: ha a hetedik helyiértékre is szükség lett volna, megszólalt egy csengő.

Az első, egységes egészként működő összeadógépet Blaise Pascal (1623 - 1662) francia matematikus, fizikus, vallásfilozófus tervezte 1642-ben. Ez a pascaline.

 

88. kép: Blaise Pascal (1623 - 1662) összeadó-gépe, a Pascaline

 

A munkát Schikardtól függetlenül végezte és gépe nem is volt olyan fejlett, mint Schikardé. A gépet Rouenben adóbeszedőként dolgozó apja számára készítette az akkor 19 éves Pascal, hogy megkönnyítse annak munkáját. A számológép megmaradt az utókornak. A számokat a gép elején lévő kerekeken kell beállítani, az eredmény pedig a gép tetején lévő kis ablakokban látszik. Ez az eszköz tízfogú fogaskerekeket tartalmaz. A fogaskerekek minden foga egy-egy számjegynek felel meg 0-tól 9-ig. Minden helyiértéknek megfelel egy ilyen fogaskerék (hatjegyű számokat lehet a géppel összeadni). A kerekek úgy kapcsolódnak össze, hogy számokat lehet összeadni vagy kivonni a fogaskerekek megfelelő számú foggal történő elforgatásával: ha a legkisebb helyiérték fogaskerekét egy foggal (36^o-kal) elfordítjuk, az a mozgásiránytól függően 1 hozzáadását vagy levonását jelenti a gépben éppen látható számból. Ebben a gépben is működik a tízesátvitel: ha az egyik helyiérték kereke a 9-es állásból a 0-ba fordul, akkor a következő nagyobb helyiérték kerekét egy foggal elfordítja.

A fordulatszámlálás fenti módja nem új találmány. Számlálásra készített szerkezet volt az alexandriai Heron úthosszmérője. A szerkezetet végigtolták a megmérendő úton. Kereke áttétellel időnként egy kicsit elfordította a felül lévő vízszintes kereket, aminek a kerületén kövek voltak elhelyezve. A gördülő kerék bizonyos számú elfordulása után a fenti vízszintes kerék éppen annyit fordult el, hogy róla leesett a következő kavics. A kavicsok egy kosárba potyogtak. Az út végén meg kellett számolni az összegyűlt kavicsokat és számukat meg kellett szorozni a gördülő kerék kerületével és az egy kő leeséséhez szükséges körülfordulások számával. Így megkapták a megtett út hosszát. Ez a berendezés az első analóg-digitál átalakítóként is felfogható.

Az 1670-es években Gottfried Wilhelm Leibniz (1646 - 1716) német filozófus és matematikus, kortársa, Pascal gépét továbbfejlesztette. Leibniz matematikai munkásságának kiemelkedõ eredményei, hogy Newtontól függetlenül 1676-ban felfedezte a differenciál- és az integrálszámítást, valamint õ tekinthetõ a matematikai logika elõfutárának. 1673-ban szerkesztett számológépéért a londoni Akadémia tagjává választotta. Ez a gép az ún. Leibniz-kerék, amelynek két példánya ma is megtekinthetõ a Hannoveri Állami Könyvtárban, két részbõl állt. Az egyik az összeadás-kivonás, a másik a szorzás-osztás elvégzésére volt alkalmas, ugyanakkor a kettõ össze is kapcsolódott. A szorzás automatizálását Leibniz ismételt összeadásokkal hajtotta végre, gépét Stepped Reckoner-nek nevezte.

 

89. kép: Wilhelm Von Leibniz (1646-1716) szorzógépe, a Stepped Reckoner

 

Ezt a gépet fejlesztette tovább Leon Bollée (1870-1913) francia autógyártó és számológép konstruktőr, aki az 1887-ben kifejlesztett gépébe beépített egy eszközt, amely a szorzótáblát tudta tárolni, ezzel téve szükségtelenné az ismételt összeadást. Bollée elõtt még Abraham Stern (1769-1842) lengyel tudós is készített egy gépet, amely már hat számjegyre végezte el a négy aritmetikai mûveletet és a négyzetgyökvonást.

A mechanikus gépek korának vége felé, az információfeldolgozás szempontjából minőségi változás a programozható számítógép ötlete. Charles Babbage (1791 - 1871) angol matematikus és korai számítógép-tudós, talán az első, akinek a programozható számítógép ötletét, sőt az automatizálás, számítógéppel vezérelt nyomtatás, ill. gyártás gondolatát köszönhetjük. Utólag megállapítható, hogy Babbage mechanikusan működő gépeinek az elve messze meghaladta korát. A brit matematikus és feltaláló tehát kidolgozta a modern digitális számítógép alapelveit. Babbage univerzális gépet tervezett, amely adatbeviteli és eredmény-kiviteli egységből, számolóműből és részeredmény-tárolóból állt volna. A gép lyukkártyákról olvasta volna be az információkat, tudott volna utasításokat és adatokat tárolni, matematikai műveleteket végrehajtani és adatokat kinyomtatni. Lyukkártyák vezérelték volna a tulajdonképpeni számítási folyamatokat is. Gépei az első mechanikus számítógépek, bár egyiket sem fejezte be teljesen. Több új típusú gépet is kigondolt.

Ilyen volt a differenciagép (Difference Engine), amit logaritmustáblázatok készítésére tervezett az 1820-as évek elején. A gép a számolás eredményét a tervek szerint pontozóval közvetlenül a nyomda által használható fémlemezbe írta volna. A differenciagép bizonyos függvényértékek (négyzetek, harmadik hatványok, logaritmusok, stb.) sorozatának kiszámítását különbségek, differenciák összeadására vezeti vissza. Babbage gépe még a hatodik rendű differenciákat is használta. Ehhez hat, egymáshoz kapcsolódó számolóművet tervezett, mai ismereteink szerint hibátlanul. A gép 20 jegyű számokkal dolgozott volna, de Babbage csak a gép egyes részeit tudta elkészíteni. A teljes terv részben anyagi okok miatt, részben pedig, a kor technikai lehetőségeinek hiányában nem valósult meg azonnal. 1834-ben a differenciagép előállítási költségeit 17 470 fontra becsülték, amikor egy gőzmozdony 1000 fontba került.

 

90. kép: Charles Babbage (1791-1871) differenciálgépének rekonstrukciója

 

Az első működő differenciagépet, Babbage készülékének egyszerűsítésével, Per Georg Scheutz (1785 - 1873) svéd jogász, nyomdász, újságíró, műfordító, feltaláló és fia, Edvard Scheutz, készítette el 1853-ban. Christel Hamann (1870-1948) tovább tökéletesítette a berendezést, és segítségével 1910-ben tízjegyű logaritmustáblázatot jelentetett meg. Differenciagépeket egészen az 1940-es évekig használtak matematikai táblázatok készítésére.

Mint említettük, a mechanikus gépek korának vége felé, az információfeldolgozás szempontjából minőségi változás a programozható számítógép ötlete, illetve a gyártási folyamatok programozása jelentette. Ez az automatizálás. Megjegyzendő, hogy a nem termelési célú folyamatok vezérlésére ill. szabályozására már évszázadok óta alkalmaztak különböző technikai megoldásokat. A zenegépekben, pl. a tüskés henger volt a jellemző megoldás, a mechanikus planetáriumok, cometariumok és az orreryk vezérlését bonyolult fogaskerék mechanizmusok végezték. A Joseph Wright of Derby (1737-1794) által taneszközként megfestett orrery készülék utódai, az 1800-as évek közepétől jól bevált szemléltető eszközök - a tellurium, lunárium, planetárium, horizontárium - lényegében kicsinyített, nem méretarányos, mechanikusan működő, „kozmikus" modellek. Ezek információtörténeti jelentősége abban is mutatkozik, hogy interpretációk; tehát szemléltető, illetve taneszköz rendszerek. Az első orrery-t egyébként, John Rowley mechanikus és George Graham órás készítette 1713-ban, az ír Charles Boyle (1676-1731), Orrery IV. earl-je megbízásából. A modern planetárium ôsét Christian Huygens (1629 - 1695) kiváló holland matematika-fizika tudós, többek közt az ingaóra szabadalmaztatója, 1682-ben készítette el. Az éggömb belsô felületére óraművel mozgatott rendszer vetítette az égitestek képeit.

 

91. kép: Christian Huygens (1629-1695) holland matematika-fizika tudós, csillagász

 

A zenegép és az orrery működését vezérlő programszerkezet feladata annak az információnak a reprodukálása, amely az azonos folyamatot lehetővé teszi, ugyanazt a dallamot, ugyanazt a bolygómozgást ismétli. Az eddig megismert mechanikus „számológépek" nagyrészt egy-egy konkrét feladat ellátása céljából jöttek létre, akár folyamatok vezérlésére, akár műveletek elvégzésére konstruálták azokat. Igazi mérföldkő a mintás anyagot előállítani képes „programozott" szövőszék, a kártyavezérlésű selyemszövő gép, amelynek létrejöttét az ipari forradalom története, a technikatörténet, a számítógép-történet, és az információtörténet sohasem mellőzheti. A termelési-gyártási folyamatok programozása és automatizálása, amelynek eredményeként gyorsabban, vagy pontosabban lehet dolgozni, napjainkban is téma. A mintás szövés vezérlésére olyan módszer kellett, amivel egyrészt hosszabb programot is meg lehet adni, másrészt pedig viszonylag egyszerűen lehet a mintát megváltoztatni, a szövőszéket "átprogramozni". Az idők folyamán többféle ilyen vezérlést találtak fel. Az osztrák Broesel 1690 körül vászonszalagra faelemeket ragasztott, ezzel határozták meg a szőtt anyag mintáját. A mintát a vászonszalagok cseréjével lehetett változtatni.

A francia Basile Bouchon 1725-ben Lyonban, a nagy textilgyári központban lyuggatott papírcsikokkal, lyukszalaggal oldja meg a vezérlést. A szintén francia Jean-Baptiste Falcon, Bouchon segédje, 1728-ban lyukkártyával vezérelhető szövőszéket készített. A szövőszéken igen sok (gyakran több ezer) szál fel-le mozgatásával alakul ki a szövet mintája; a lyukkártya a szálak mozgatásához szükséges információt hordozza. A kártyán egyfajta táblázat található, amely megmutatja, hogy a különböző munkafázisokban a szálaknak milyen helyzetben kell lenniük. A kártyát letapogató berendezés érzékeli, hogy a táblázat adott cellájában van-e lyuk, és eszerint állítja be a szálat. A lyukak mindkét megoldás esetén horgokat állítanak be, ezek emelik, vagy süllyesztik azután a láncfonalakat. A gépek fél-automatikusan üzemelnek: a kártya vagy a papírcsík előtolását még kézzel kell végezni. A teljesen automatikus, lyukszalag vezérlésű szövőgépet Jacques de Vaucanson (1709-1782) fejlesztette ki 1745-ben.

Elődei munkáit Joseph Marie Jacquard (1752-1834) szintetizálja, 1790-ben kezdi el építeni a lyukkártyás vezérlésű, tetszőlegesen bonyolult mintázat létrehozására alkalmas szövőgépét, amelyet a forradalom miatt, csak 1801-ben tud véglegesíteni, és a párizsi kiállításon bemutatni. Minden esetre, tény, hogy a textiliparban máig jacquard-berendezésnek neveznek minden olyan szerkezetet, amely valamilyen módon egyedileg vezérel bizonyos szerkezeti elemeket - a szövőgépen a nyüstszálakat, a kötőgépen tűket, a fonatológépeken a babákat - függetlenül attól, hogy a régebbi gépeken valóban még lyukkártyás vagy lyukszalagos megoldást, az újabb gépeken pedig számítógépes vezérlést alkalmaznak-e. Az is tény, hogy Jacquard előtt minden mintaváltást kézzel kellett beállítani, s időközben ez az új konstrukció igen sok régi szövőszéket kiszorított, 1812-ben már közel 12.000 Jacquard-féle szövőgép üzemel.

 

92. kép: Joseph Marie Jacquard (1752-1834) lyukkártya vezérlésű szövőgépe

 

Az első, valóban programozható gép Jacquard szövőszéke után nem sokat váratott magára. Jacquard munkája azonban túlmutat a textiliparon, bár a mai értelemben nem nevezhető programozásnak, mivel a szövőszék „programja", vagyis a lyukkártyák dekódolásának módja, nem változtatható. A kártyán, illetve szalagon csak bemeneti adatok találhatóak. Mint korábban említettük, a lyukkártyás vezérlést alkalmazta később, a 19. század második felében Charles Babbage ún. analitikai gépén, amely a számítógépek egyik ősének tekinthető, majd Herman Hollerith azon a gépén, amelyet eredetileg az 1890. évi USA-beli népszámlálás eredményeinek feldolgozására fejlesztett ki és amely később világszerte elterjedt az adatfeldolgozásban. Ennek információtörténeti jelentőségére még visszatérünk.

 

93. kép: Herman Hollerith (1860-1929) táblázatkezelő gépe 1889-ből

 

E fejezetet azzal zárjuk, amellyel a következő fejezetünket kezdhetnénk: sok történész Babbege-et és a munkatársát, Lady Augusta Ada Byron (1815-1852) matematikust, Lord Byron angol költő lányát, tartja a modern digitális számítógép igazi feltalálójának. Tanítómestere a jól ismert matematikus, Augustus de Morgan, az ő felesége révén került kapcsolatba Babbage-dzsel. Augusta Ada Lovelace az olasz mérnök, Luigi Menabrea (1809-1896) által Babbage differenciagépéről írt francia nyelvű beszámolót angolra fordította, és felvette a kapcsolatot a konstruktőrrel, aki megkérdezte, hogy miért nem írt inkább egy eredeti cikket. Lady Lovelace erre elkészítette a cikk bővített, az eredetinél háromszor hosszabb változatát. Részletesen leírta például, hogy miként lehet Bernoulli-számokat számítani az „Analytical Engine" segítségével. Írásában összehasonlítja a számológépet Jacquard 1801-es szövőszékével: "Ez algebrai mintákat sző, ugyanúgy, ahogy Jacquard szövőszéke virágokat és leveleket". Ada Lovelace javasolta Babbage-nak, hogy ne decimális, hanem bináris formában tárolja a számokat. Ugyancsak ő találta ki, hogy hogyan lehetne a géppel egy utasítás-sorozatot többször végrehajtatni, ezért ő az „első programozó", a computer. Ada grófnő először fogalmazta meg a ciklus és a szubrutin fogalmát, jegyzi meg Szűcs Ervin professzor. Ada Lovelace-ről nevezték el később az Ada programnyelvet.